Blow Moulding Process: Parts, Working Principle, Defects, Advantages, Disadvantages & Applications [PDF]
Blow Moulding is a manufacturing process by which hollow plastic products can be obtained. It is also used for forming plastic containers, plastic buckets, bottles, or other hollow shapes.
It is applicable for thermoplastics only.
We already had an article on the Injection Moulding Process, and Compression Moulding whereas, in today's paper, we are going to discuss Blow Moulding Process along with its Parts, Working Principle, defects, Advantages, Disadvantages & Applications.
Blow Moulding Diagram:
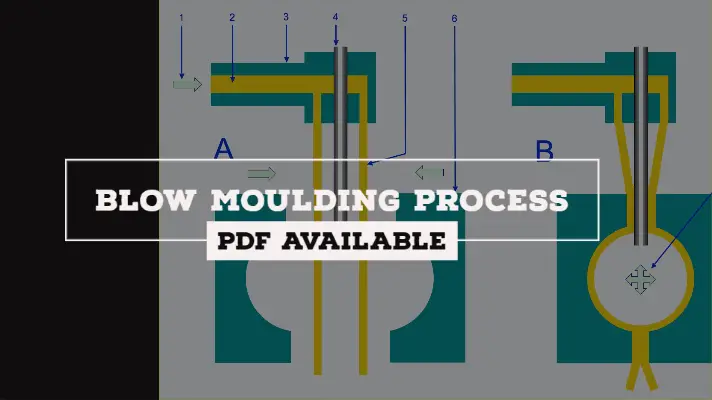
The parts of Blow Moulding Diagram are shown below.
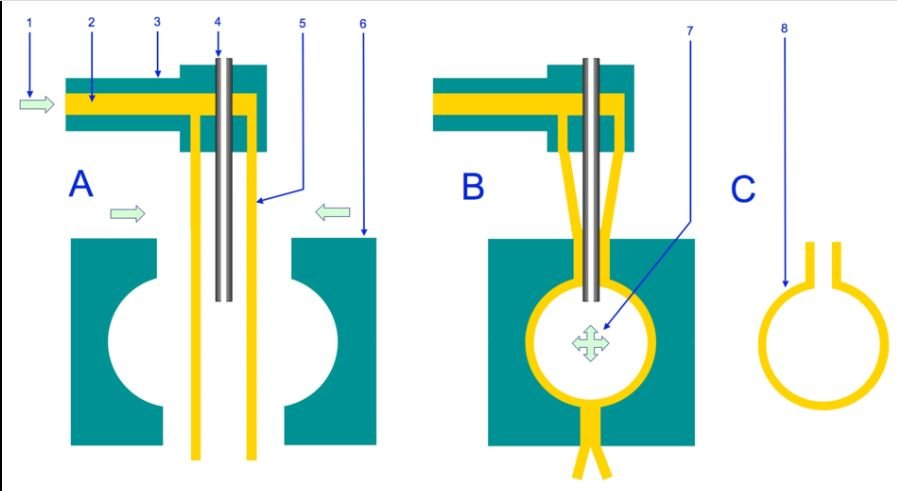
Parts of Blow Moulding Process:
The parts of Blow Molding process are as follows:
- The feed from the Extruder
- Melted Plastic
- Extruder Head
- Airtube
- Parison
- Mould
- Air Pressure
- End Product.
Explanation for the Parts of Blow Moulding Process:
The explanation for the parts of Blow Molding is as follows.
1. The feed from the Extruder:
Extruder is simply a machine which consists of cylinders and barrels where the plastic is to be heated up.
The Feed from the Extruder is given as an input into the Blow Molding Machine.
2. Melted Plastic:
Melted plastic acts as a medium for the creation of plastic hollow components.
3. Extruder Head:
Melted plastic has to be sent to the extruder head so that it can be passed through various other channels.
4. Air tube:
The air tube is used to pressurize the air when the molted plastic enters into the mold cavity [Link to Science Direct] and it is about to bulge.
5. Parison:
It is a Tubular shape of hot plastic with a hole at one end through which compressed air can pass.
6. Mould:
Mould cavity consists of patterns where molten plastic is to be deposited and solidification takes place and after solidification, final product is obtained.
7. Air Pressure:
When the molten plastic enters from the parison into the mould cavity, air pressure is forced into the cavity such that the molten plastic touches the mould corners and thereafter solidification takes place.
8. End Product:
Finally the end product is obtained after the solidification.
Next dive into the working principle of Blow molding process.
Working Principle of Blow Moulding Process:
The Overview of all the parts of Molding Machine is shown in the above diagram under Segment A.
The Feed from the Extruder is given as an input into the Blow Molding Machine. The feed acts as the melted plastic and it is to be passed through the extruder head section and forming it into a parison.
The parison is a tube-like piece of plastic with a hole at one end through which compressed air can pass. The parison is to be passed through the mold.
The Cope and Drag portions of mold are to be pressed against each other and at the same time compressed air is to be passed from the air tube as shown in segment B.
By blowing high-pressure air on the soft sheet (parison), it will bend according to the internal shape of the mold and deposits on the internal surface of the mold and achieve the shape of the component.
By the cooling process, the prosuct will regain its hardness.
This is how you can get the final product in the segment C as shown in the above figure.
Blow Molding Pressure Distribution:
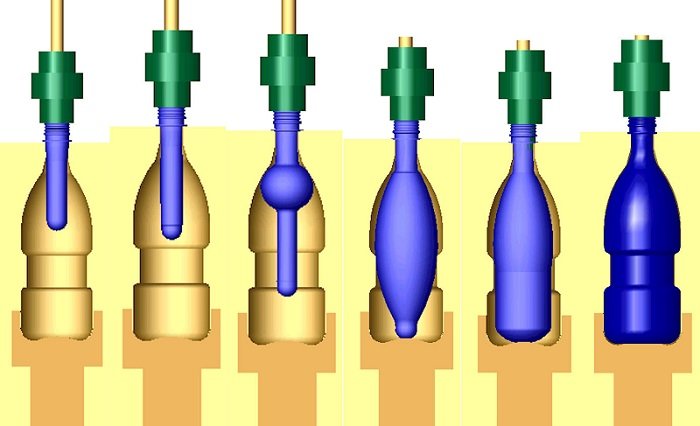
Do you know how the pressure distribution takes place in the Blow molding process?
- Water Bottles; P<1 bar
- Plastic Buckets; P= 1-2 bar
- Large Liquid Containers; P= 2-5 bar
The simple analysis of the component can be produced with a good dimensional accuracy of the product.
Defects of Blow Moulding:
The defects of Blow Molding Process are as follows:
- Thickness and too much flanging of components
- Deep vertical stripes
- Volume reduction of blow molding components
- high fluctualtion will be seen in the quality of Blow Molding Components.
- wall thickness is non-uniform.
Advantages of Blow Moulding Process:
The Advantages of Blow Moulding Process are as follows.
- To produce high thickness plastic parts, high blowing pressure is required.
- Fast production rate.
- Recycling can be done
- low tool cost in the case of the Blow Moulding process.
Disadvantages of Blow Moulding Process:
The disadvantages of Blow Moulding Process are as follows.
- Difficult to produce Complex geometry of the components with good dimensional accuracy.
- It can be applied only for hollow parts.
- Thick parts cannot be manufactured.
- If the shape of the mold is complex ->result distribution is non-uniform->compaction of the film is non-uniform-> thickness is non-uniform and -> dimensional accuracy is low.
Applications of Blow Moulding Process:
The applications of Blow Moulding Process are as follows.
By this process we can able to make:
- Water Bottles
- Plastic Buckets
- Liquid Containers
- Plastic Cups
- Mugs etc.
Difference between Injection Molding and Blow Molding:
Blow molding is used to produce hollow containers, such as bottles. On the other hand, injection molding is used to produce solid pieces, such as solid plastic plates used in the kitchen.
Watch a Video on Blow Moulding Process:
What is the difference between Blow Moulding and injection Moulding?
What is the most common type of blow molding process?
What is Moulding and types of Moulding?
What are the types of Moulding?
More Resources:
Injection Moulding Process
Compression Moulding Process
References [External Links]:
- Blow Mould Tool Design-Journal
- Blow Molding-PDF