Topics of Today
In thermodynamics, there are four laws, which are called the Laws of Thermodynamics. Today in this article we will be going to discuss these four thermodynamics laws in a detailed manner.
The four laws of thermodynamics are as follows.
So let me give you a brief overview of all!
Zeroth's Law of Thermodynamic states that when body ‘A’ is in thermal equilibrium with body ‘B’ and also separately with body ‘C’ then B and C will be in thermal equilibrium with each other.
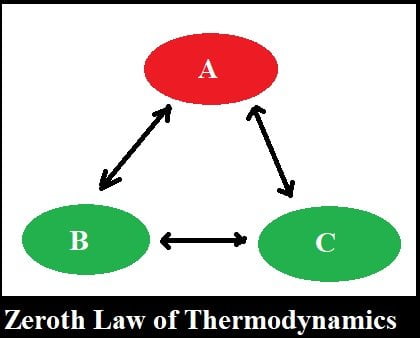
(or) If two systems are in thermal equilibrium with a third system, they must be in thermal equilibrium with each other.
The bodies A & B are said to be in thermal equilibrium with each other if and only if, the final temperatures of both the bodies will be the same when they are kept near to each other.
The first law of thermodynamics is also called as law of conservation of energy.
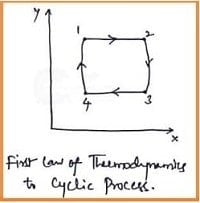
The first law of thermodynamics can be applied to the Cyclic and Non-Cyclic processes. Let's discuss the first law of thermodynamics to a cyclic process and is as follows.
During any cycle that a closed system undergoes, the network transfer is equal to the net heat transfer.
Q-W= ΔE
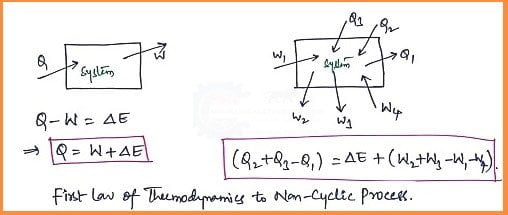
If there are more energy transfer quantities (i.e. Energy transfer and Work transfer) involved in the process as shown in the figure. Then the equation is as follows.
(Q2 +Q3 -Q1)= ΔE +(W2+W3-W1-W4)
The Non-Flow Processes are as follows.
The detailed explanation of all the Non-Flow processes is as follows.
Volume (V) = Constant
In a constant Volume process, the working substance is to be placed in the container and the boundaries of the system are immovable and thereby no work is said to be done on or by the system. Fig. below shows the Isochoric Process.
Considering the mass of the working substance as 'unity' and applying the First Law of Thermodynamics. The derivation for the Reversible Constant Volume Process is shown below.
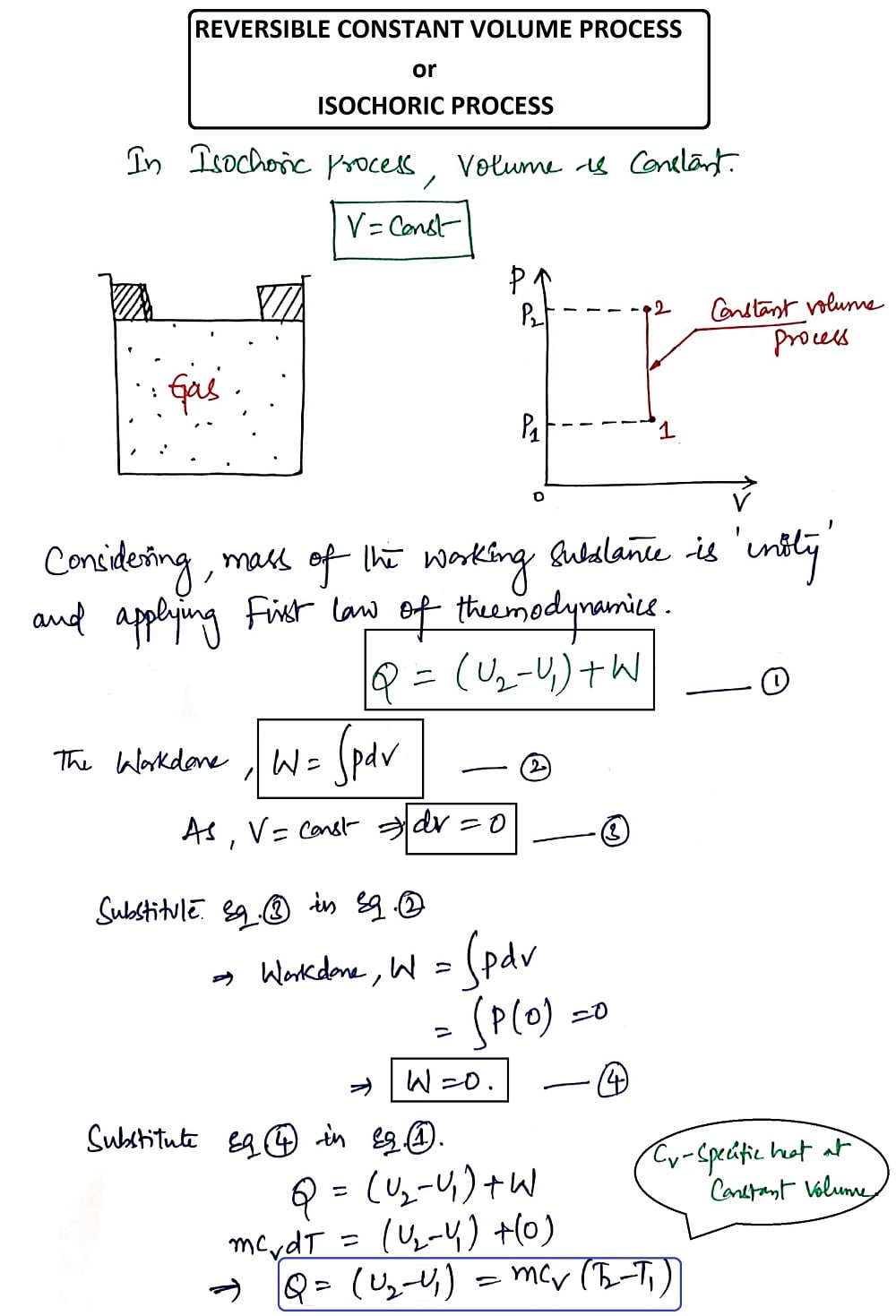
Thus from the Isochoric Process, we get the heat Q as
Q= (U2-U1)= mCv(T2-T1)
Where
Cv-Specific heat at Constant Volume
U-Internal Energy
T1, T2-Temperatures
Pressure (P)= Constant
As it is a Constant Pressure process, the gas present in the cylinder pushes the piston from its initial position to the final position because of movable boundaries and it indicates the work is done by the gas on its surroundings.
In this process, the Pressure is kept Constant whereas, the Volume increases from V1 to V2.
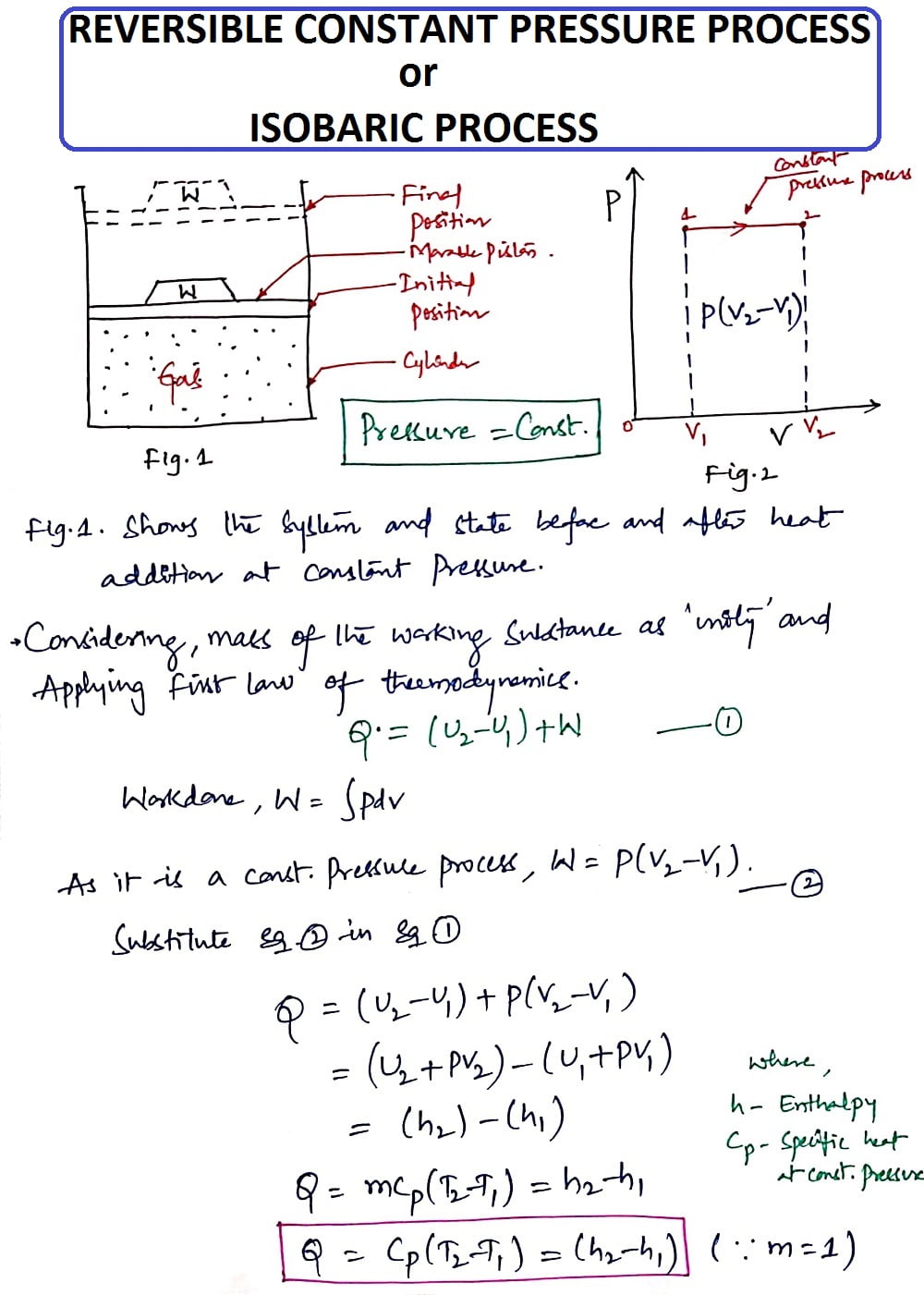
Thus from the Isobaric Process, we get the heat Q as
Q = Cp(T2-T1) = (h2-h1)
Where
Cp-Specific heat at Constant Pressure
h-enthalpy
T1, T2-Temperatures
Temperature (T) = Constant
The Governing equation for Isothermal Process is PV=C
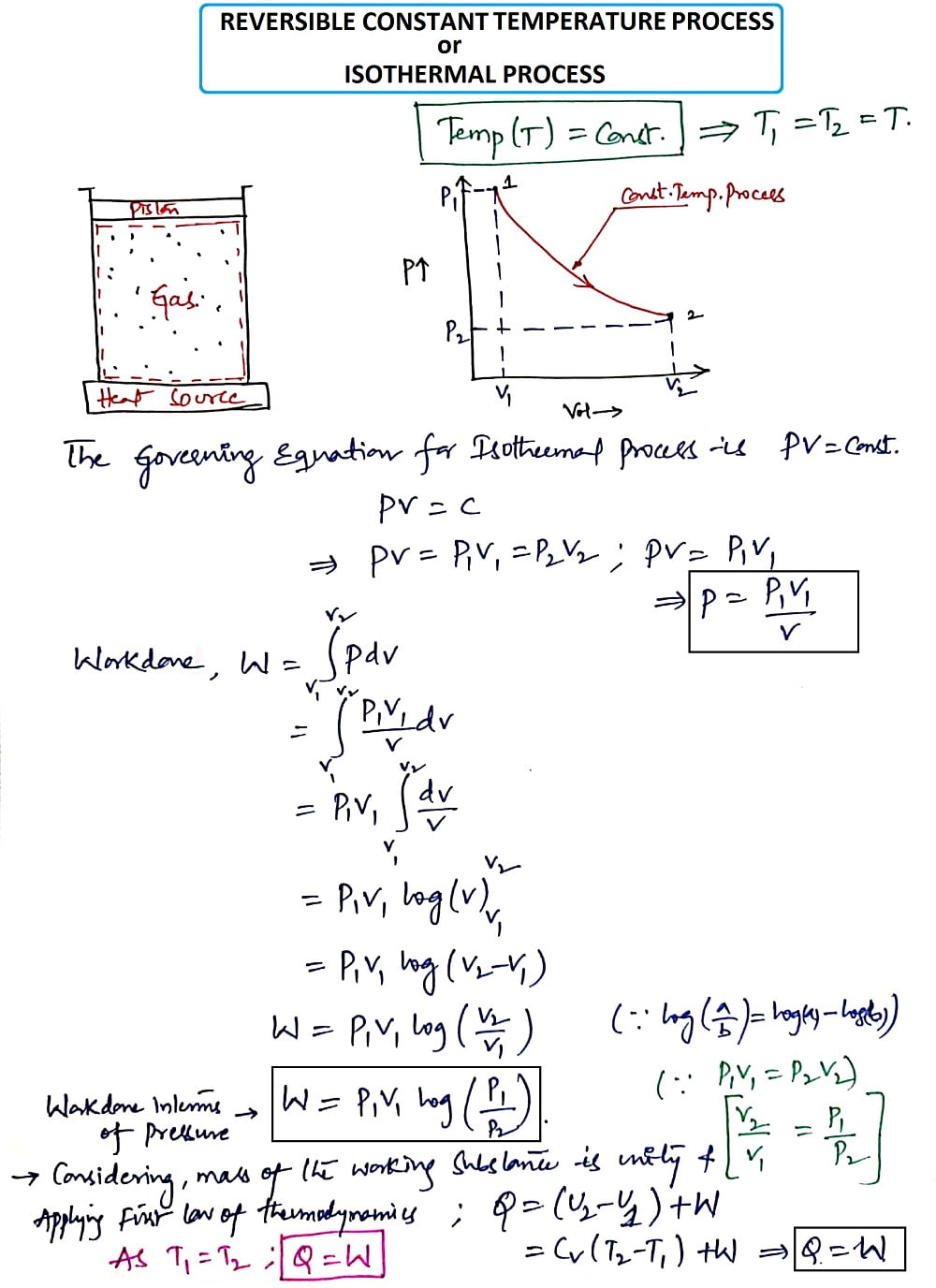
Thus from the Isothermal Process, we get the heat Q as
Q = Cv(T2-T1) +W
But, it is a constant Temperature process i.e. T1= T2, thus we get
Q=W
Where W= Work done
Heat Transfer (Q)= Zero
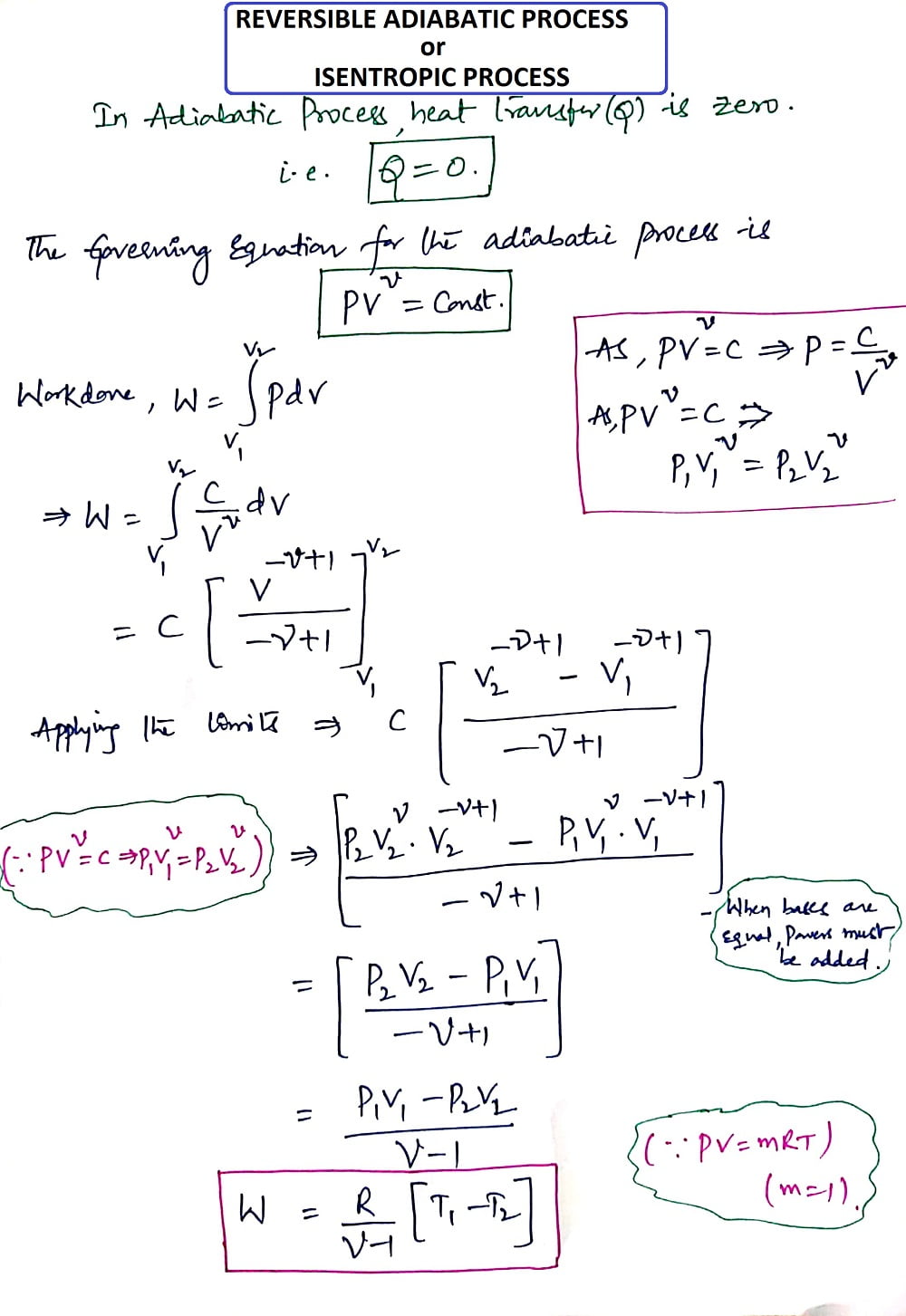
Considering the Unit mass of the working substance and Applying First Law of Thermodynamics.
Q= (U2-U1) + W
As it is an Adiabatic process, put Q = zero, then we get
U1-U2= W= (R/γ-1 ) * [T1-T2]
This is the derivation of the Reversible Adiabatic process or Isentropic process.
Next, we can dive into the Polytropic Process where we can discuss the derivation of the Polytropic process with respect to Isobaric, Isochoric, and Isothermal Processes.
An expansion process in which the energy to do work is supplied partly from an external source and partly from the gas itself known as Polytropic Process and that follows a path that will fall in between those of Isothermal and Adiabatic Process.
For any reversible process,
Work done, W=∫ P dv
The governing equation for the polytropic process is PVn = Constant. Where n is the Polytropic Index.
The derivation of the Polytropic Process is explained below in a written format.
In a Polytropic process, the polytropic index(n) can take the value from -∞ to +∞. Now place the values of n and get Isobaric, isothermal, adiabatic, and Isochoric processes which were explained below.
Thus we had completed the derivation part of the Polytropic Process. Let's go head towards Second Law and Third Law of Thermodynamics.
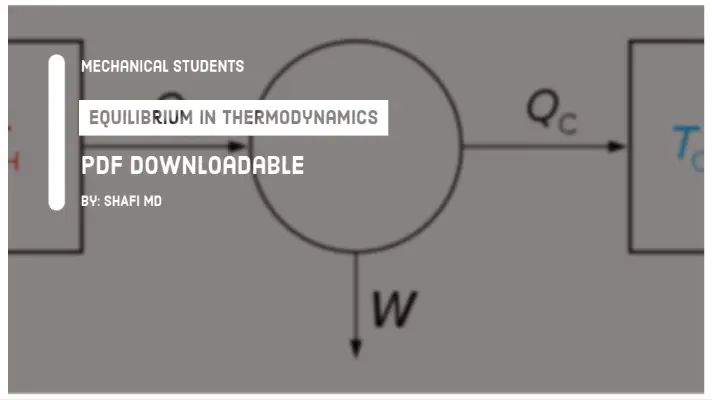
According to the second law of thermodynamics, the whole heat energy cannot be converted into work and part of the energy must be rejected to the surroundings.
The figure below shows the possible machine in which heat is supplied from the hot reservoir, work is done on the surroundings and remaining is rejected to cool reservoir (mostly the atmosphere).
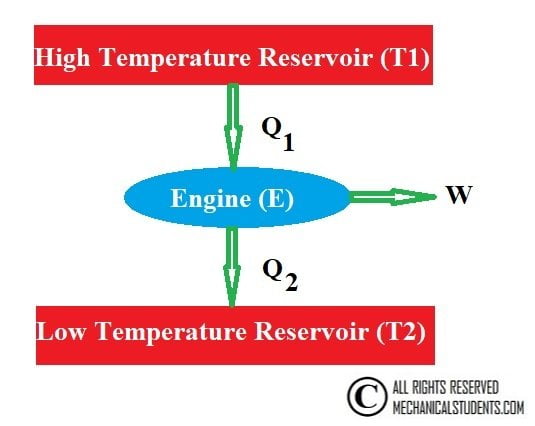
The work is said to be high-grade energy and heat is low-grade energy. The complete conversion of low-grade energy into higher grade energy in a cycle is impossible.
There are two statements of the 2nd Law of Thermodynamics those are:
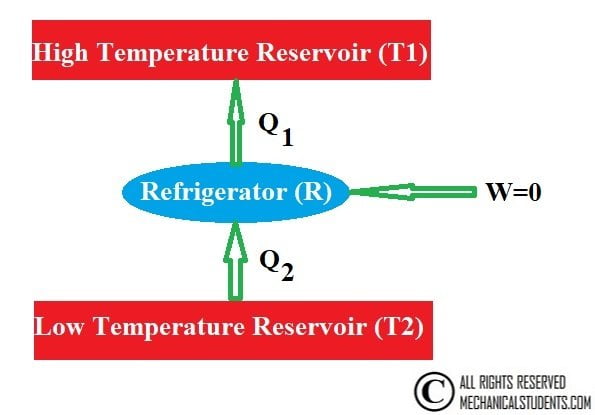
It is impossible for a self-acting machine working in a cyclic process, unaided by any external agency to convey heat from a body at a lower temperature to a body at a high temperature.
Or
It is impossible to construct a refrigerator whose only purpose is the absorption of heat from a low-temperature reservoir and its transfer to the high-temperature reservoir without any work input.
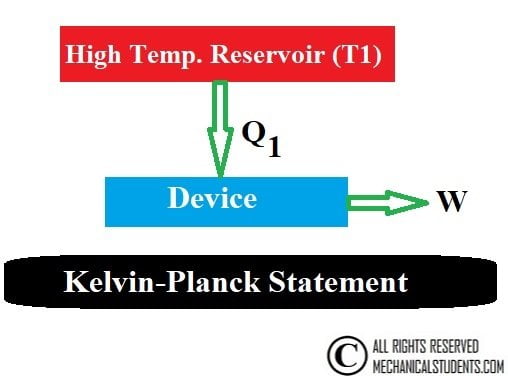
It is impossible to construct an engine which while operating in a cycle produces no other effect except to extract heat from a single reservoir and produce work.
Or
It is impossible to construct an engine whose only purpose is the absorption of heat from a high-temperature reservoir and its conversion to work.
For Example, Heat engine.
Any device which converts 100% heat to 100% work is called the Perpetual motion machine of the second kind and the second law tells us that, Perpetual motion machine of the second kind is impossible.
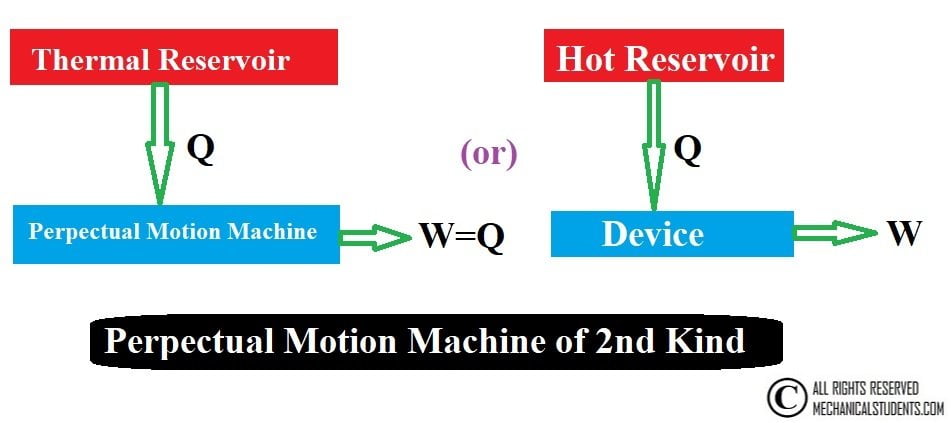
Without violating the first law, a machine can be imagined which would continuously absorb heat from a single thermal reservoir and would convert this heat completely into work. The efficiency of such a machine would be 100%.
This machine is called the Perpetual motion machine of the second kind. A machine of this kind will evidently violate the second law of thermodynamics.
The third law of thermodynamics states that the entropy of a system at absolute zero is a well-defined constant.
"The change in entropy is equal to the heat absorbed divided by the temperature of the reversible process".
ΔS = Q/T
Q= Heat Absorbed
T= Temperature
ΔS= Change in Entropy
The higher the entropy, the less energy is available in your system to do work.
When the temperature approaches absolute zero, then the entropy of a system approaches a constant value.
∮(δQ/T) ≤ 0.
The following conditions are as follows.
This is the explanation of all laws of Thermodynamics I.e. Zeroth law, First Law, Second Law, and Third law of thermodynamics in a detailed way.
If you have any doubts, you can ask us and we will reply to you as soon as possible.
More Resources:
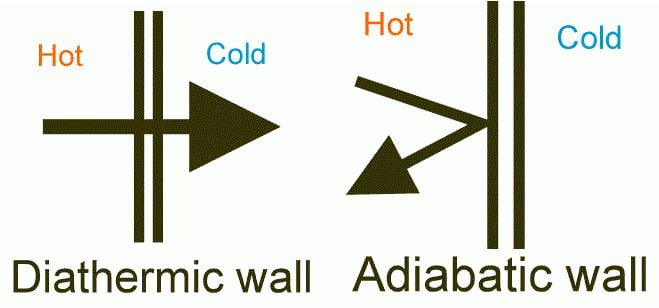
What is the Difference Between Diathermic and Adiabatic Process?
Otto Cycle
Diesel Cycle
Carnot Cycle
I found the note on thermodynamics very useful, thanks.