Carnot Cycle Notes [Complete Explanation] with [PDF]

Hello readers, In the last session, we had completed the derivation on Otto Cycle and Diesel Cycle whereas in today's session, we will discuss the explanation of Carnot Cycle along with its derivation.
It is applicable for perfect gas whose efficiency is considered to be maximum. It was proposed by 'Sadi Carnot' in 1824.
Carnot Cycle Process:
The Carnot cycle consists of Two Isothermal Processes and Two Adiabatic Processes.
Both these processes are reversible and therefore It is the most efficient cycle, as it involves no losses.
The theoretical heat engine that operates on this cycle is the Carnot Engine.
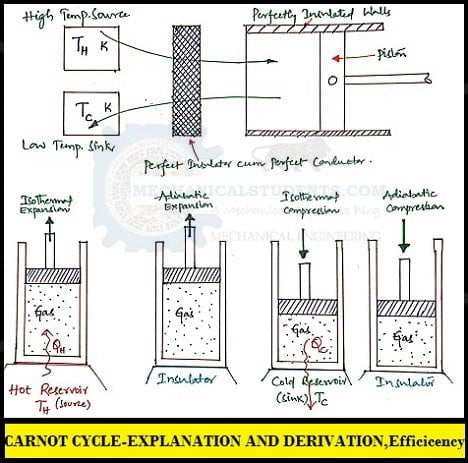
Assumptions:
- The working material should be a perfect gas.
- The motion of the piston in the cylinder is frictionless.
The working substance(gas) is to be placed in the cylinder, which expands and compresses and makes the piston to move up and down w.r.t. the processes.
It consists of 4 reversible processes. They are
- Process 1-2: Reversible Isothermal Expansion.
- Process 2-3: Reversible Adiabatic Expansion
- Process 3-4: Reversible Isothermal Compression.
- Process 4-1: Reversible Adiabatic Compression.
The explanation of the above processes are as follows.
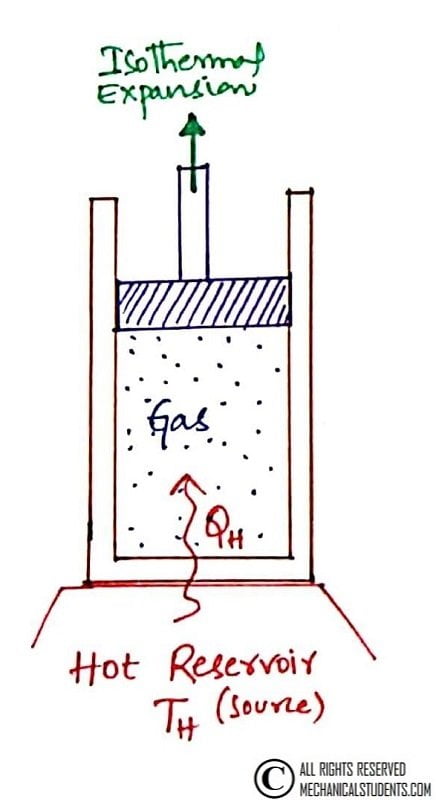
Process 1-2: Reversible Isothermal Expansion
This is a Reversible Isothermal Expansion process. In this process, initially at state 1, the temperature of the gas is T1 and the cylinder head is in contact with a hot body or hot reservoir or Source also at a temp T1.
Heat is supplied to the system(gas) from the source(high temp reservoir/hot body) at Constant temperature i.e. T1 = T2 and the expansion has taken place.
Due to this, there is a pressure drop from P1 to P2 and the increase in entropy from S1 to S2 which indicates that the work is done by the gas.
Process 2-3: Reversible Adiabatic Expansion
This is a Reversible Adiabatic Expansion process. At state 2, the hot reservoir is replaced by insulation. There is no heat transfer during this process.
Even though work is done by the gas i.e. due to internal energy and as there is no heat transfer, the temperature within the system is used to do the work and thereby at the end of this process, there is a drop in temperature i.e. from T2 to T3(shown in T-S Diagram).
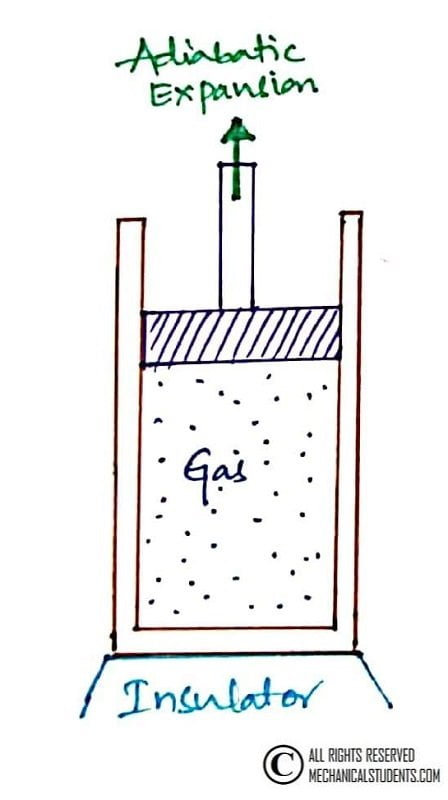
Whereas the volume is increased from V2 to V3, Pressure decreases from P2 to P3, and entropy remains constant i.e. S2 = S3.
Process 3-4: Reversible Isothermal Compression
This is a Reversible Isothermal Compression process. In this process, the insulation at the cylinder head is removed and the cylinder head is brought into contact with a cold reservoir or sink.
Heat is rejected from the gas to the sink(low temp reservoir or cold body) at Constant temperature i.e. T3=T4(shown in T-S Diagram)
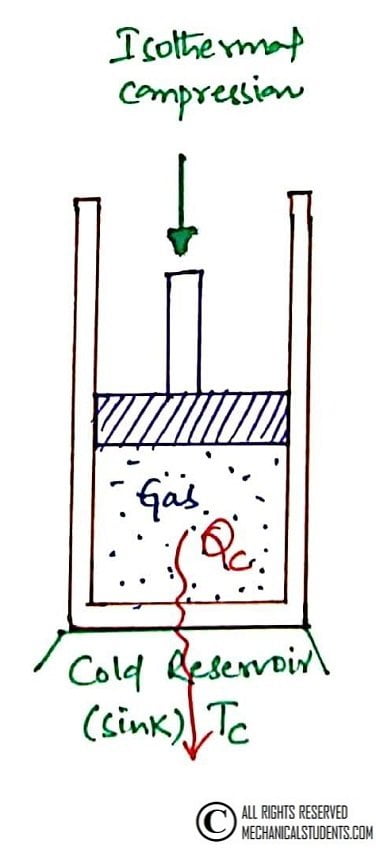
Here, Pressure is increased from P3 to P4, Entropy decreases from S3 to S4, and Volume is decreased from V3 to V4.
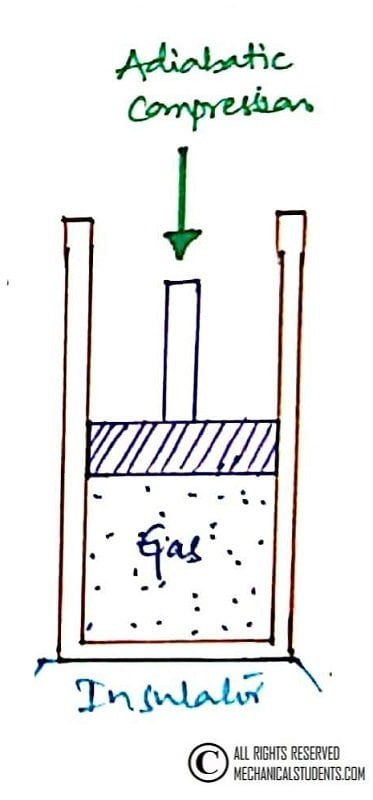
Process 4-1: Reversible Adiabatic Compression.
This is a Reversible Adiabatic Compression process. In this process, the cold reservoir is replaced by the insulation so that the entire system becomes adiabatic.
No heat transfer(adiabatic) takes place during this process and temperature increases from T4 to T1, Pressure increases from P4 to P1, Volume decreased from V4 to V1 and Entropy remains constant S1=S4.
The P-V and T-S Diagram for Carnot cycle are shown below. The derivation of the Carnot cycle is explained below to determine Thermal efficiency.
Carnot Cycle Derivation:
The Carnot Cycle derivation was presented below in a written format.
Thermal Efficiency = Workdone/Amount of heat supplied
Work done (W) = Heat supplied(Qs)-Heat rejected(QR)
Now project the values into the equation and get the thermal efficiency which is shown below.
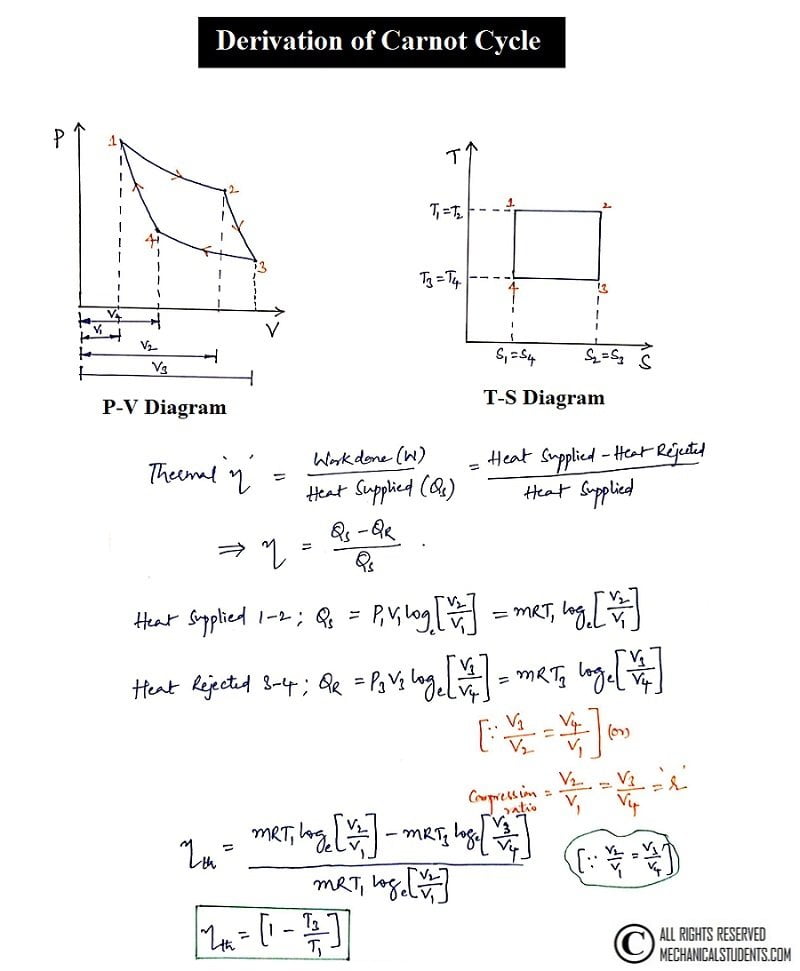
The Thermal Efficiency of the Carnot cycle is derived above and the equation of thermal efficiency is [1-(T3/T1)].
So I hope you are able to understand the topic that is the Carnot Cycle. If you have any doubts regarding this paper, feel free to ask me in the comment section.
FAQ's on Carnot Cycle:
What are the four process of Carnot cycle?
Process 1-2: Reversible Isothermal Expansion.
Process 2-3: Reversible Adiabatic Expansion
Process 3-4: Reversible Isothermal Compression.
Process 4-1: Reversible Adiabatic Compression.
What is meant by Carnot cycle?
What is the use of Carnot cycle?
More Resources:
Otto Cycle Derivation
Diesel Cycle Derivation