Refrigeration: Definition, Types, Classification of Refrigerants, Advantages, Disadvantages, and Applications [PDF]

The equipment used for removing the heat continuously for maintaining a low temperature in a space is called 'refrigerator'. In the last session, we had discussed Vapor Compression Refrigeration Cycle and in today's session, we can discuss in detail the concept of Refrigeration along with its Definition, Unit, Classification of Refrigerants and Applications.

Let's start with the definition.

Definition of Refrigeration:

Refrigeration may be defined as a process of removing heat from a substance and pumping it to the surroundings. It also includes the process of maintaining and reducing the temperature of a body below the general temperature of its surroundings.

Thus in a refrigerator heat is prepared from low temperature to high temperature. Theoretically, the refrigerator is a heat pump which pumps heat from a cold body and delivers it to a hot body.

Lets see the terms involved in Refrigeration.

What is Refrigeration Cycle?

Equipment used for removing the heat continuously for maintaining a low temperature in a space is called 'refrigerator' and the Cycle on which it operates is called the refrigeration cycle.

What are Refrigerants?

The working fluids used for carrying away heat are called 'refrigerants' which are used in both refrigeration and air conditioning.

What is Air Conditioner?

The equipment used for air conditioning is called an air conditioner.

What is Unit of Refrigeration?

The unit of refrigeration is expressed in terms of "Tonne of Refrigeration" (TR).

One Ton of refrigeration: It can be defined as the amount of refrigeration effect produced by the uniform melting of one tone of ice (1000 kg) from and at 0°C in 24 hrs.

1 Tonne of refrigeration (TR)= (335x1000)/ 24

where latent heat of ice= 335 KJ/Kg= 13958.333 KJ/hr= 13958.333/24 KJ/min

1 Tonne of refrigeration (TR)= 232.6 KJ/min

Coefficient of Performance of a Refrigerator:

The performance of a refrigeration system is expressed by a term known as the coefficient of performance(C.O.P.)

It is the ratio of heat extracted in the refrigerator to the work done on the refrigerant. It is also known as the theoretical coefficient of performance.

Theoretical C.O.P= Heat extracted/ Work done = Q/W

Relative C.O.P= Actual C.O.P / Theoretical C.O.P

Methods for Refrigeration:

The various methods of Refrigeration are as follows.

• Refrigeration by evaporation
• Refrigeration by ice
• Refrigeration by the expansion of air
• Refrigeration by throttling process
• Refrigeration by dry ice
• vapor Refrigeration system

Lets see the Types of Refrigeration in detail.

Types of Refrigeration:

There are various types of Refrigeration Cycles but majorly Two types of Refrigeration are important and are as follows.

1. Vapor Absorption Refrigeration Cycle
2. Vapor Compression Refrigeration Cycle

The explanation for the above types of Refrigeration cycles are as follows.

Vapor Absorption Refrigeration Cycle:

In the Vapor Absorption process, the compression process of the vapor compression cycle is replaced by an absorber, a generator, and a pump.

The principle of the system is to make use of two substances that can be separated when heated.

The two substances can be

1. Ammonia (Refrigerant) and
2. Water (Absorbent).

Components of Vapor Absorption Refrigeration Cycle:

The components of Vapour Absorption Refrigeration Cycle are as follows.

• Condenser
• Expansion Valve
• Evaporator
• Absorber
• Pump
• Generator

Working of Vapor Absorption Refrigeration Cycle:

In this type of refrigeration system, the vapor produced in the evaporator passes into the absorber.

The absorber consists of a homogeneous mixture of ammonia and water known as aqua ammonia. In the absorber, the vapor is absorbed and released from the absorbent, which maintains constant low pressure.

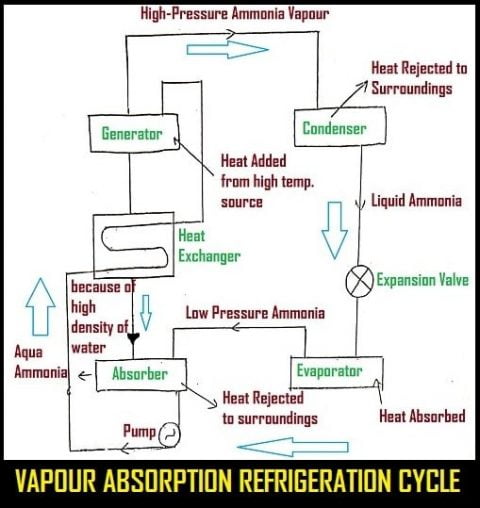
This process takes place at a temperature slightly above that of the surroundings.

In this process, some heat is transferred to the surroundings. The strong ammonia solution is then pumped through a heat exchanger to the generator by a pump where high pressure and temperature are maintained.

The ammonia vapor enters into the condenser where it gets condensed into liquid ammonia.

The liquid ammonia which is at high pressure is passed through an expansion valve through which wet Ammonia vapor, at low temperature and pressure, comes out.

The vapor is then passed through the evaporator. The evaporator absorbs heat and is dried. The dried vapor is again taken to the absorber and thus the cycle is completed.

The Coefficient of Performance of the Vapor Absorption Refrigeration System is as follows.

C.O.P= (Heat absorbed during evaporation)/(work done by the pump + heat supplied in the heat exchanger)

This is the explanation of the Vapour Absorption Refrigeration cycle. Let's see the explanation of the Vapor Compression Refrigeration cycle.

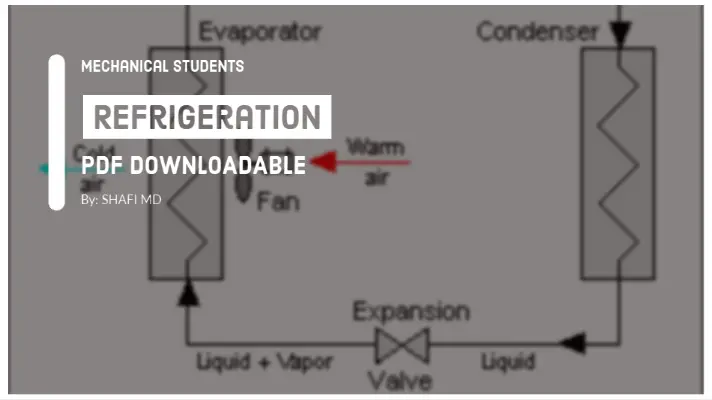
Vapor Compression Refrigeration Cycle:

This cycle is widely used compared to the Vapor Absorption Refrigeration cycle. The components of the Vapor Compression Refrigeration cycle are Compressor, Condenser, Receiver, Expansion Valve, and Evaporator.

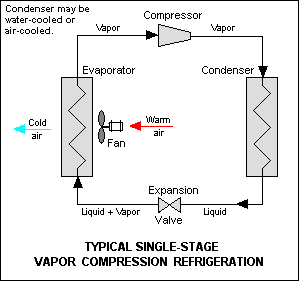
The working of Vapor Compression Refrigeration System can be completed under 4 processes and are Compression, Condensation, Expansion and Vapourization process.

The Coefficient of Performance(C.O.P) of a Simple Vapor Refrigeration Cycle is

C.O.P. = (heat extracted or refrigerating effect)/Work done.

C.O.P. = (h2-h4)/(h3-h2).

The detailed explanation of Vapor Compression Refrigeration cycle is here

Now let's see about Refrigerants and its classification.

Refrigerants:

Any substance which in the refrigeration system absorbs heat from a low-temperature system and delivers the heat so absorbed to a higher temperature system is referred to as a refrigerant.

Classification of Refrigerants:

There are two types of Refrigerants and are as follows.

1. Primary Refrigerants
2. Secondary Refrigerants

Primary Refrigerants:

The working mediums or heat carries which directly take part in the refrigeration system and cool the substance by the absorption of latent heat are called as Primary refrigerants.

Example of Primary Refrigerants are Ammonia, SO2, CO2, Methyl chloride, etc..

Secondary Refrigerants:

These are circulating substances that are first cooled with the help of primary refrigerants and then employed for cooling purposes.

Example of Secondary Refrigerants are Ice, Solid CO2, etc..

Now lets see the desirable properties of Refrigerants in terms of physical, chemical and Thermodynamic properties.

Properties of Refrigerants:

The properties of Refrigerants are classified as

• Chemical Properties of Refrigerants
• Physical Properties of Refrigerants
• Thermodynamic Properties of Refrigerants

Lets see one by one.

Chemical Properties of Refrigerants:

The Chemical Properties of Refrigerants are as follows.

• Non-toxic
• Non-flammable and non-explosive
• Non-corrosive to metal

Physical Properties of Refrigerants:

The Physical Properties of Refrigerants are as follows.

• Low specific heat
• A low specific volume of vapor
• Low viscosity

Thermodynamic Properties of Refrigerants:

The Thermodynamic Properties of Refrigerants are as follows.

• Low freezing point
• Low boiling point
• High latent heat of vaporization

Other Properties of Refrigerants:

The various other properties of Refrigerants are as follows.

• Ease of leakage location
• Availability and low cost
• High COP

These are the various properties of Refrigerants and now we can see the applications of Refrigeration.

Advantages of Refrigeration System:

The Advantages of Refrigeration are as follows.

• The basic advantage of air refrigeration is the working substance which is always available in the atmosphere.
• The refrigerant (air) is free of cost and the system is simple to understand.
• The refrigerant keeps the container cool by breaking the bacterial involvement.
• There is no danger of fire due to the leakage of refrigerant from the pipes(if any).

Disadvantages of Refrigeration System:

The Disadvantages of Refrigeration System are as follows.

• The running cost of the refrigeration is high because the Coefficient of Performance(C.O.P) is very low.
• Per One Tonne of refrigeration, the quantity of refrigerant used is high compared to other systems.
• In Environment, as the air contains moisture which can affect the danger of frosting at the valves.

Applications of Refrigeration System:

The applications of Refrigeration System are as follows.

Refrigeration is extensively used for increasing the storage life of perishable items especially food products, vegetables, fruits, milk, beverages, chilling of water, ice formation, etc.

Industrial applications include chemical manufacturing, petroleum refinery, petrochemical plants, paper, and pulp industry, etc.

• Ice making
• Manufacturing and treatment of metals
• Industrial air-conditioning
• Transportation of food
• Chemical and related industries
• Freezing food products
• Medical and surgical aids
• Central air-conditioning

This is the detailed explanation of Refrigeration. If you have any doubts, you can ask us and we will reply to you as soon as possible.

FAQs:

More Resources:

Vapour Compression Refrigeration Cycle
Summer and Winter Air Conditioning

References [External Links]:

• Refrigeration-PDF
• Unit 5: Refrigeration Systems - IGNOU